My road from AI Engineer to Number Theorist
Code is unreasonably helpful in exploring Math
After 10 years of software engineering with a focus on responsible AI, I lost the thrill. What started off as an exciting challenge to overcome became a scoping session and a few weeks of checking off boxes. The fun of coding projects came from mentoring bright eyed and bushy tailed software engineers through the excitement of overcoming a challenge in Privacy Preserving Machine Learning.
How was I going to bring back the excitement of sucking at something?
Study the hardest subject in college. Obviously.
While at MIT, I almost failed the Discrete Mathematics course: 6.042.
It was a hard pill to swallow that changed my whole trajectory in college. This course is strictly easier than any of the introductory math major courses and I scored 30 points below the average of 95 on the first exam.
My exam session was also labeled too easy so the other session’s average (higher than my score) was bumped up to match my sessions average. Ouch. But, luckily, by the end of the class my final exam score bumped me up into a passing C.
My only C other than Senior Spring Chemistry.
I came to realize recently why. MIT gave me a week to catch up. I never took any logic or proofs fundamentals course beforehand. Proofs seemed to be pulled out of thin air.
Recently, I started the MIT Math curriculum as an independent study.
However, this time around, I am expanding the first week of each of the courses into a pre-course book.
Helpful books to onramp into pure math
For proofs, I found How to Read and Do Proofs. A little orange book that would have changed my major.
The best part is that the book’s density increases over time. The appendix, although most people probably skip it, is much closer to the texts I struggled with in my first attempt at pure math.
It reads really easily and covers the first lecture of most of the other pre course books I am currently reading.
Abstract Algebra by Judson is another pre book. MIT uses Artin for 18.701, which is very hard to read in my opinion. I will be going through it next, I am on chapter 16 of Judson’s. It is perfect for software engineer’s looking to learn Abstract Algebra. Coding Theory was covered in College but from the applied side. Burnside’s Counting Theorem was super interesting.
It also covered RSA, which I learned in 6.042, however, the clarity of Euclid’s Algorithm and fast modular exponentiation algorithm gave me a deeper understanding. I implemented the whole RSA chapter in python to make sure I understood it. I will be sharing a deep dive in a future post.
Elementary Number Theory by Burton was recommended to me by a Cryptographer friend. I am on chapter 8. Frankly, it was a hard read at first. I first attempted it over two years ago. And it prompted me to look for a pre book. Luckily after How to Read and Do Proofs I was able to make more progress on it. It is still a harder read than Abstract Algebra but given how dense it is, every few pages sends me on a mathematical tangent.
Number Systems and the Foundations of Analysis by Mendelson was recommended by a Quora rabbit hole I went down. It reminds me of How to Read and Do Proofs but it is centered on the preparations for Analysis. The book is a slower take on the foundations of 18.100a. 18.100a, Analysis at MIT, has an amazing lecture series that I have been enjoying as well.
Outside of books I tend to distract myself with trying to reformulate extremely hard famous problems.
Mathematical Tangents
I became slightly obsessed with representing perfect powers as series. I wrote induction proofs for n**2
\(n^{2} \;=\; \sum_{i=1}^{n} \bigl(2i - 1\bigr) \)- \(n^{3} \;=\; \sum_{i=0}^{n-1} \!\left( 6\,T_i + 1 \right) \)
And my continual exploration of Euler’s Phi function and its connection to Goldbach’s Conjecture. I will go deeper into this later but the crux of the idea is that the relative primes in the Euler Totient sum up to the target number. For 104:
By pigeonhole principle this implies that there is a prime pair. My program found a few portions of numbers where the property may not be holding, I need to verify it further but it seemed like an interesting spin on a problem. I am researching that formulation applied to numbers of the form 2**n*p and looking into whether there are number theoretic functions for a lower bound on composite pairs of that form.
Computer guided independent study
At first, I mostly spent my time using pen and paper to study. After a while I wanted feedback and found Lean4. It has been a whole new element to my study practice. If I find a pattern in a sequence, I am able to use induction to prove it. But, what if I made a mistake? I have no advisor to reach out to.
That is where Lean4 has helped. Lean4 is a coding language with a built in Theorem checker. I checked a few of my induction proofs and am using it to formalize proofs that I want to build on. I will share more about Lean4 and how I use it to build out my own Math world. One of my next books is How To Prove It by Velleman because of it’s integration with Lean4.
I am also almost done with the Natural Number Game, and will also look into more levels on https://adam.math.hhu.de/#/g/leanprover-community/nng4
Python for conjecture validation has helped me expand on or disprove my ideas quickly. I can also visualize ideas where, writing them out by hand would take some time. Here is a table I made to find patterns in composite pairs within Euler’s Totient for 2**n*13. My program found that an invariant I thought would hold might not work for higher powers of 2. I need to verify the code further to see why the property does not hold.
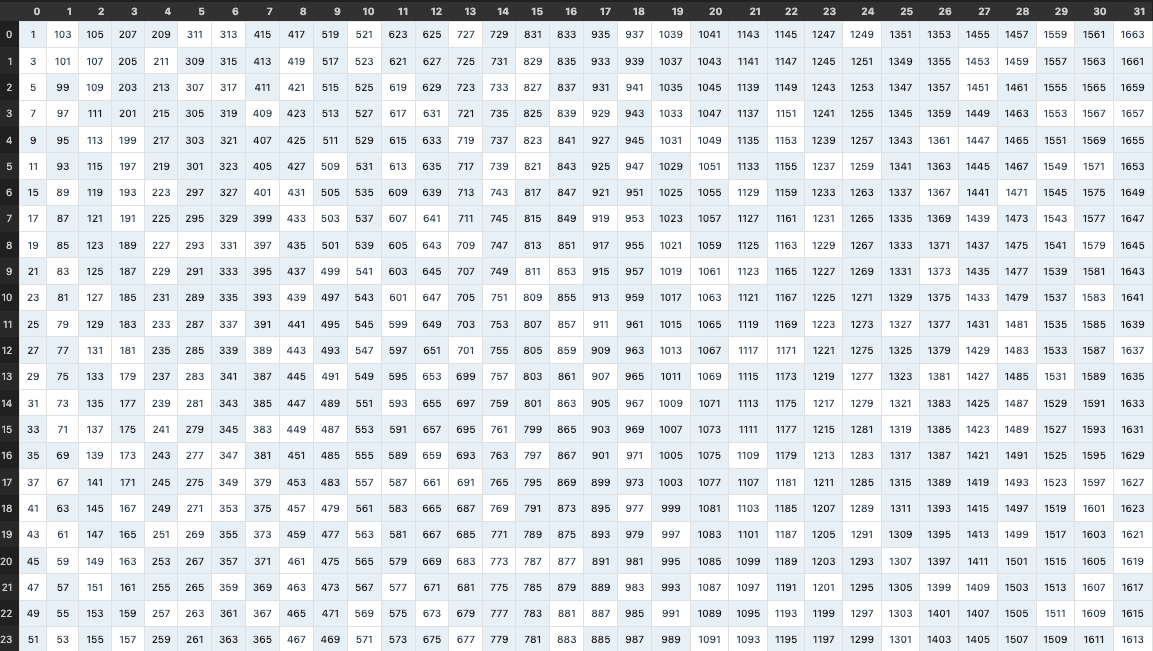
Each visualization I make will help me explore future problems. It is also much easier to build nowadays. For now, I am reformulating elementary questions. Over time, I will expand my scope and hopefully find a little corner of research to contribute to.
Regardless, I am excitedly learning new Math each day. Code is helping me explore ideas early on. And I am allowing myself to take pre-courses to prepare for books that are currently out of my range.
If you are interested in following along as I cover the Pure Math curriculum for Number Theory subscribe for more updates and learnings.
Keep Exploring.